Jason的小世界
首页
归档
标签
分类
日志
关于
avatar
文章
17
标签
9
分类
6
首页
归档
标签
分类
日志
关于
目录
  1. 一、栈的概念
  2. 二、利用python建立栈
  3. 三、队列的概念
  4. 四、队列的链式表示和实现—-链队列
python数据结构之栈和队列
|数据结构
阅读量:

一、栈的概念

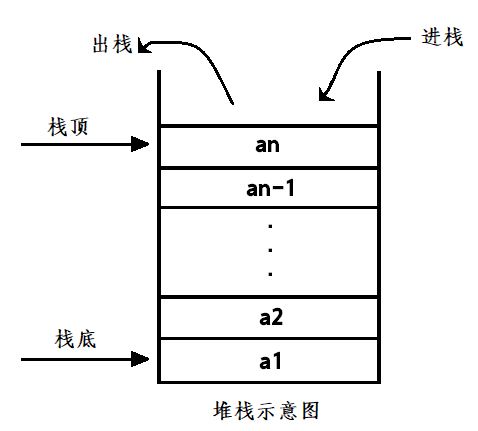
栈（stack）又名堆栈，它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。这一端被称为栈顶，相对地，把另一端称为栈底。
栈的特点：
1.元素是一前一后、一对一的关系
2.有两端：栈底、栈顶
3.操作受限：插入和删除都只能在栈顶进行

27fBcT.jpg

二、利用python建立栈

python并没有内建栈，但是我们可以利用列表实现栈的模拟。
入栈即往列表内添加元素，可以用append()方法，出站即把列表中的最后一个元素删除并返回相应的值，可以用pop()方法。
栈的简单应用-中缀表达式转后缀表达式
设一般数学表达式的运算符包括 +、-、*、/ 四种，当然允许（），且（）优先级高。为方便实现，设定输入的表达式只允许个位整数。要求设计一个完整的程序，对输入的一个日常的中缀表达式，先转换成后缀表达式，然后计算该后缀表达式的值，输出相关结果信息。
如：
输入中缀表达式：2*（3+4）-（8-3）/5
转换后缀表达式：234+*83-5/-
表达式结果：13

python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
def opcom(ch1,ch2):
    s1=['+','-','*','/','(',')','#']
    s2=[['>','>','<','<','<','>','>'],
        ['>','>','<','<','<','>','>'],
        ['>','>','>','>','<','>','>'],
        ['>','>','>','>','<','>','>'],
        ['<','<','<','<','<','=',' '],
        ['>','>','>','>',' ','>','>'],
        ['<','<','<','<','<',' ','=']]
    i=s1.index(ch1)
    j=s1.index(ch2)
    return s2[i][j]

def postfix(s):
    mystack = []
    d = []
    mystack.append('#')
    num = ['0','1','2','3','4','5','6','7','8','9']
    for i in range(len(s)):
        c = s[i]
        if c in num: #判断是否是操作数
            d.append(c)
        elif c == ')': #如果读入的是')'
            while True:
                if mystack[-1] != "(":
                    d.append(mystack.pop())
                else:
                    mystack.pop()
                    break
        else:
            top = mystack[-1] #栈顶元素
            k = opcom(top,c) #判断优先级
            if k == '<': #高于栈顶运算符
                mystack.append(c)
            elif k == '>': #低于栈顶运算符
                while True:
                    if opcom(mystack[-1],c) == '>':
                        d.append(mystack.pop())
                    elif opcom(mystack[-1],c) == '=': #top和c都为'#'的情况
                        break
                    else:
                        mystack.append(c)
                        break
            elif k == '=':
                mystack.pop()
            else:
                print("此中缀表达式中有错误！")
    return d        
def result(v):
    mystack = []
    a = []
    b = []
    num = ['0','1','2','3','4','5','6','7','8','9']
    for i in range(len(v)):
        c = v[i]
        if c in num:
            mystack.append(c)
        else:
            b = mystack.pop()
            a = mystack.pop()
            count = eval(a+c+b)
            mystack.append(str(count))
    return mystack[-1]

                
if __name__ == "__main__":
    #s = '(((6+((2*9)/3))+(4*2))-8)#'
    #s = '(1+2)*3+4/(5+6*7)+8#'
    #s = '((1+(2*(1+3)))-(4/2))#'
    #s= '(((1+2)*3)-5)#'
    s = '((2*(3+4))-((8-3)/5))'
    try:
        v = postfix(s)
		print("中缀表达式：{}".format(s.strip("#")))
        print('转换后的右缀表达式为：')
        for i in v:
            print(i,end='')
        print()
        print("运算结果为：")
        print(result(v))   
    except:
        print("此中缀表达式中有错误！")

运行结果：

python
1
2
3
4
5
中缀表达式：((2*(3+4))-((8-3)/5))
转换后的右缀表达式为：
234+*83-5/-
运算结果为：
13.0

为方便栈的基本操作，可以建立以下方法：
Stack() 建立一个空的栈对象
push() 把一个元素添加到栈的最顶层
pop() 删除栈最顶层的元素，并返回这个元素
peek() 返回最顶层的元素，并不删除它
isEmpty() 判断栈是否为空
size() 返回栈中元素的个数
汇总成一个栈的类：

python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Stack:
    """模拟栈"""
    def __init__(self):
        self.items = []
        
    def isEmpty(self):
        return len(self.items)==0 
    
    def push(self, item):
        self.items.append(item)
    
    def pop(self):
        return self.items.pop() 
    
    def peek(self):
        if not self.isEmpty():
            return self.items[len(self.items)-1]
        
    def size(self):
        return len(self.items)

三、队列的概念

队列是一种特殊的线性表，特殊之处在于它只允许在表的前端（front）进行删除操作，而在表的后端（rear）进行插入操作，和栈一样，队列是一种操作受限制的线性表。进行插入操作的端称为队尾，进行删除操作的端称为队头。
队列的特点：
1.元素仍是一前一后、一对一的关系
2.有两端：队头、队尾
3.操作受限：队尾进元素（插入）、队头出元素（删除）。即一头进一头出
274ZFA.jpg

队列的应用
【例】银行业务取票排队
【例】医院挂号
【例】机票、火车票等订票
【例】汽车加油站
【例】打印机缓冲区

队列的基本操作运算：
creat() 创建一个空队列
enqueue() 新元素入队列，即参与排队
dequeue() 删除队头元素，即队头元素出队列
isempty() 判断队列是否为空
isfull() 判断队列是否已满
frontval() 查看队头元素，但不出队列
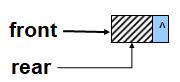
利用python的列表（list）来实现队列，同时设立front和rear两个指示器（int变量）分别指向队头元素的前一个位置和队尾元素的位置（下标）。
建立队列：

python
1
2
q = []
front=rear=-1

空队标志：

python
1
front= =rear

入队：

python
1
2
rear+=1  `    
q[rear]=x

出队：

python
1
2
front+=1     
x=q[front]

汇总如下：

python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
MAXSIZE=100       #定义队列的最大容量
q=[None]*MAXSIZE    #队列的数组声明
front=-1
rear=-1       #队列初始状态

#入队操作，item入队列
def enqueue(item):
    global MAXSIZE
    global rear
    global q
    if rear=MAXSIZE-1:
        print(“队列已满！”)
    else:
        rear=rear+1   #修改位置
        q[rear]=item  #入队

#出队操作
def dequeue():
    global front
    global rear
    global q
    if rear==front:
        print(“队列已空！”)
    else:
        front=front+1   #修改位置
        return q[front]  #出队

但是，利用列表会存在溢出问题：
①真溢出,真满

python
1
2
front==-1
rear==MAXSIZE-1

②假溢出,假满

python
1
2
front != -1
rear==MAXSIZE-

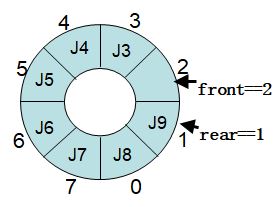
解决的方法－－循环队列
关键：利用“模”运算
1.入队：

python
1
2
rear=(rear+1)%MAXSIZE;
q[rear]=x;

2.出队：

python
1
2
front=(front+1)%MAXSIZE; 
x=q[front];

3.队列为空条件：

python
1
front==rear

4.队列为满的条件：

python
1
(rear+1)%MAXSIZE==front

5.当前队列元素个数：

python
1
(rear-front+MASXIZE)%MAXSIZE

2Xd3r9.jpg
汇总如下：

python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
MAXSIZE=100       #定义队列的最大容量
q=[None]*MAXSIZE    #队列的数组声明
front=rear=-1       #队列初始状态

#入队操作，item入队列
def enqueue(item):
    global MAXSIZE
    global rear
    global q
    if (rear+1)%MAXSIZE==front:
        print(“队列已满！”)
    else:
        rear=(rear+1)%MAXSIZE   
        #修改入队位置
        q[rear]=item  #入队

#出队操作
def dequeue():
    global front
    global rear
    global q
    if rear==front:
        print(“队列已空！”)
    else:
        front=(front+1)%MAXSIZE   
        #修改位置
        return q[front]  #出队元素返回

四、队列的链式表示和实现—-链队列

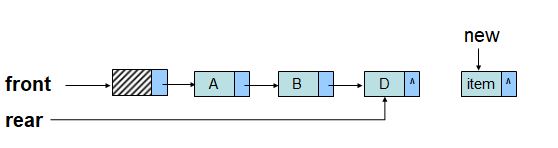
与单链表结构一样，用一带头结点的单链表表示队列，成为链队列。显然，需要两个分别指向对头和队尾的指针，并约定头指针端为队头。
由此，链队列的结构与单链表一样，唯一区别在于操作不同，是单链表插入和删除的特殊情形。
入队：就是在链表表尾插入元素，即rear后面插入一结点
出队：就是删除表头元素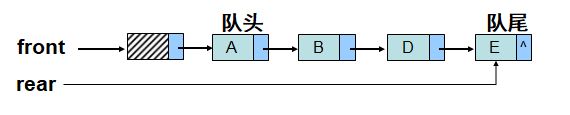
2XwZsH.jpg
链队列结构（类）的声明

python
1
2
3
4
5
6
7
class  Qnode:
      def __init__(self,data,next=None):
           self.data=data  #元素的值
           self.next=None #指针

front=Qnode()   #头结点
rear=front          #空队列

2Xwbmd.jpg
链队列入队

python
1
2
3
4
5
6
7
8
def  EnQueue(item):
     global front
     globa rear
     new=Qnode() #生成新结点
     new.data=item
     new.next=None
     rear.next=new #链入rear后面
     rear=new    #当前元素为队尾

2X0Gh6.jpg
链队列出队

python
1
2
3
4
5
6
7
8
9
def  DeQueue ():
     global front
     global rear
     if front==rear:
          print(“队列已空！”)
     else：
          item=front.next.data   #取队头元素值
          front.next=front.next.next  #删除队头元素
          return item

2X00HA.jpg
链队列的变化—-循环队列
用一个带头结点的循环链表来表示循环队列，且该队列只设尾指针。
2X0fBj.jpg

文章作者: J.M.
文章链接: https://www.masj.top/post/3f968a68.html
版权声明: 本博客所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Jason的小世界！
python 程序进阶
相关推荐
2021-06-09
python数据结构之数组结构
2021-06-10
python数据结构之链表
2020-02-05
python之Matplotlib库绘图
2019-07-31
python之os库
2019-01-30
python之异常处理
2019-01-31
python之文件处理
繁